Surfaces isométriques

Quand on froisse une feuille de papier, des plis se forment et s'assemblent à partir de points coniques (voir Fig. 1). De façon étonnante, ce sont ces défauts ponctuels qui contrôlent le froissage du papier. Une très belle illustration consiste à appuyer avec la pointe d'un crayon sur un disque de papier simplement posé sur une tasse.

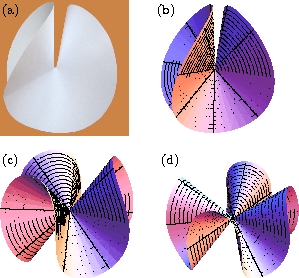
Fig. 1: Papier froissé	Fig. 2: L'e-cône

Ces défauts coniques qui apparaissant dans le papier sont assez différents de nos cornets de glace qui eux sont plutôt obtenus en supprimant un secteur angulaire d'un disque plan et en collant les deux bords créés. Si au contraire on ajoute un secteur angulaire, on obtient une infinité de formes possibles sans aucun besoin d'équilibrer par des forces externes. Sur la Fig. 2 on voit des exemples de ces e-cônes (e comme excédentaires). Certaines algues marines, par exemple, adoptent spontanément ces formes durant leur développement.

En utilisant la géométrie différentielle un modèle simple est developpé pour déterminer la forme de ces e-cônes et les contraintes élastiques engendrées. Les résultats théoriques se comparent favorablement à de simples expériences faites avec du papier. La forme symétrique à deux plis est la forme de plus basse énergie.

Publications sur ce thème (en anglais)

• Isometric bending requires local constraints on free edges
  Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo

  While the shape equations describing the equilibrium of an unstretchable thin sheet that is free to bend are known, the boundary conditions that supplement these equations on free edges have remained elusive. Intuitively, unstretchability is captured by a constraint on the metric within the bulk. Naïvely one would then guess that this constraint is enough to ensure that the deformations determining the boundary conditions on these edges respect the isometry constraint. If matters were this simple, unfortunately, it would imply unbalanced torques (as well as forces) along the edge unless manifestly unphysical constraints are met by the boundary geometry. In this article, we identify the source of the problem: not only the local arc-length but also the geodesic curvature need to be constrained explicitly on all free edges. We derive the boundary conditions which follow. In contrast to conventional wisdom, there is no need to introduce boundary layers. This framework is applied to isolated conical defects, both with deficit as well, but more briefly, as surplus angles. Using these boundary conditions, we show that the lateral tension within a circular cone of fixed radius is equal but opposite to the radial compression, and independent of the deficit angle itself. We proceed to examine the effect of an oblique outer edge on this cone perturbatively demonstrating that both the correction to the geometry as well as the stress distribution in the cone kicks in at second order in the eccentricity of the edge.
  
  Math. Mech. Solids, 24: 4051, 2019. Cf. aussi arXiv:1904.05855.
  

   

• Dipoles in thin sheets
  Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller

  A flat elastic sheet may contain pointlike conical singularities that carry a metrical "charge" of Gaussian curvature. Adding such elementary defects to a sheet allows one to make many shapes, in a manner broadly analogous to the familiar multipole construction in electrostatics. However, here the underlying field theory is non-linear, and superposition of intrinsic defects is non-trivial as it must respect the immersion of the resulting surface in three dimensions. We consider a "charge-neutral" dipole composed of two conical singularities of opposite sign. Unlike the relatively simple electrostatic case, here there are two distinct stable minima and an infinity of unstable equilibria. We determine the shapes of the minima and evaluate their energies in the thin-sheet regime where bending dominates over stretching. Our predictions are in surprisingly good agreement with experiments on paper sheets.
  
  Eur. Phys. J. E, 36: 106, 2013. Cf. aussi arXiv:1212.3262.
  

   

• Conical instabilities on paper
  Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo

  The stability of the fundamental defects of an unstretchable flat sheet is examined. This involves expanding the bending energy to second order in deformations about the defect. The modes of deformation occur as eigenstates of a fourth-order linear differential operator. Unstretchability places a global linear constraint on these modes. Conical defects with a surplus angle exhibit an infinite number of states. If this angle is below a critical value, these states possess an n-fold symmetry labeled by an integer, n ≥ 2. A nonlinear stability analysis shows that the 2-fold ground state is stable, whereas excited states possess 2(n - 2) unstable modes which come in even and odd pairs.
  
  J. Phys. A: Math. Theor., 45(1): 015203, 2012. Cf. aussi arXiv:1107.5008.
  

   

• Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
  Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann

  We investigate the morphology of thin discs and rings growing in circumferential direction. Recent analytical results suggest that this growth produces symmetric excess cones (e-cones). We study the stability of such solutions considering self-contact and bending stress. We show that, contrary to what was assumed in previous analytical solutions, beyond a critical growth factor, no symmetric e-cone solution is energetically minimal any more. Instead, we obtain skewed e-cone solutions having lower energy, characterized by a skewness angle and repetitive spiral winding with increasing growth. These results are generalized to discs with varying thickness and rings with holes of different radii.
  
  Phys. Rev. Lett., 105(6): 068101, 2010. Cf. aussi arXiv:1007.1871.
  

   

• Conical Defects in Growing Sheets
  Martin Michael Müller, Martine Ben Amar, Jemal Guven

  A growing or shrinking disc will adopt a conical shape, its intrinsic geometry characterized by a surplus angle φ_e at the apex. If growth is slow, the cone will find its equilibrium. Whereas this is trivial if φ_e≤0, the disc can fold into one of a discrete infinite number of states if φ_e is positive. We construct these states in the regime where bending dominates, determine their energies and how stress is distributed in them. For each state a critical value of φ_e is identified beyond which the cone touches itself. Before this occurs, all states are stable; the ground state has twofold symmetry.
  
  Phys. Rev. Lett., 101(15): 156104, 2008. Cf. aussi arXiv:0807.1814.
  

   

• How paper folds: bending with local constraints
  Jemal Guven, Martin Michael Müller

  A variational framework is introduced to describe how a surface bends when it is subject to local constraints on its geometry. This framework is applied to describe the patterns of a folded sheet of paper. The unstretchability of paper implies a constraint on the surface metric; bending is penalized by an energy quadratic in mean curvature. The local Lagrange multipliers enforcing the constraint are identified with a conserved tangential stress that couples to the extrinsic curvature of the sheet. The framework is illustrated by examining the deformation of a flat sheet into a generalized cone.
  
  J. Phys. A: Math. Theor., 41(5): 055203, 2008. Cf. aussi arXiv:0712.0978.